
异常值的产生的原因/影响
我们通常把偏离整个样本总体的观测值称为异常值.
数据输入误差: 指在数据收集, 输入的过程中, 人为错误造成的误差. 比如某人的月收入是1W, 因为人为错误的多敲了一个0, 则月收入了变成了10W, 这个样本相比较其他样本是异常的.
测量误差: 这个是最常见的误差来源, 比如某个测量仪器损坏了, 那个这个仪器的所有测量值都是有误差的.
有意造成的误差: 当某些数据存在敏感信息会产生此类误差, 通常是认为原因故意造成的.
数据处理误差: 在操作数据或者提取数据的时候造成的误差.
异常值对模型的预测和分析的影响主要有增加错误方差, 降低模型的拟合能力; 异常值的非随机分布会降低正态性, 这会影响很多统计学模型的基本假设.
异常值的检测
一般采用可视化的方法就可以进行异常值的检测,如箱线图。它可以显示基本的统计数据,比如异常值, 最小值, 最大值, 四分位数等。
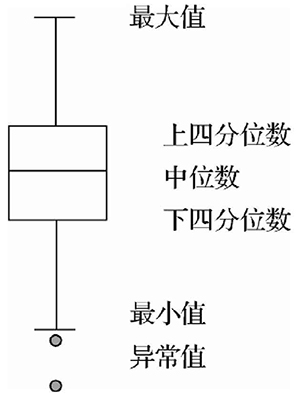
利用箱线图可以使用以下几个原则来判定异常值:
1.封顶方法,即不在5和95百分位之外的都算异常值。
2. 在距离均值三倍标准差以外的都算异常值。
3. 不在-1.5*IQR 和 1.5*IQR 之间的样本也可以认为是异常值。
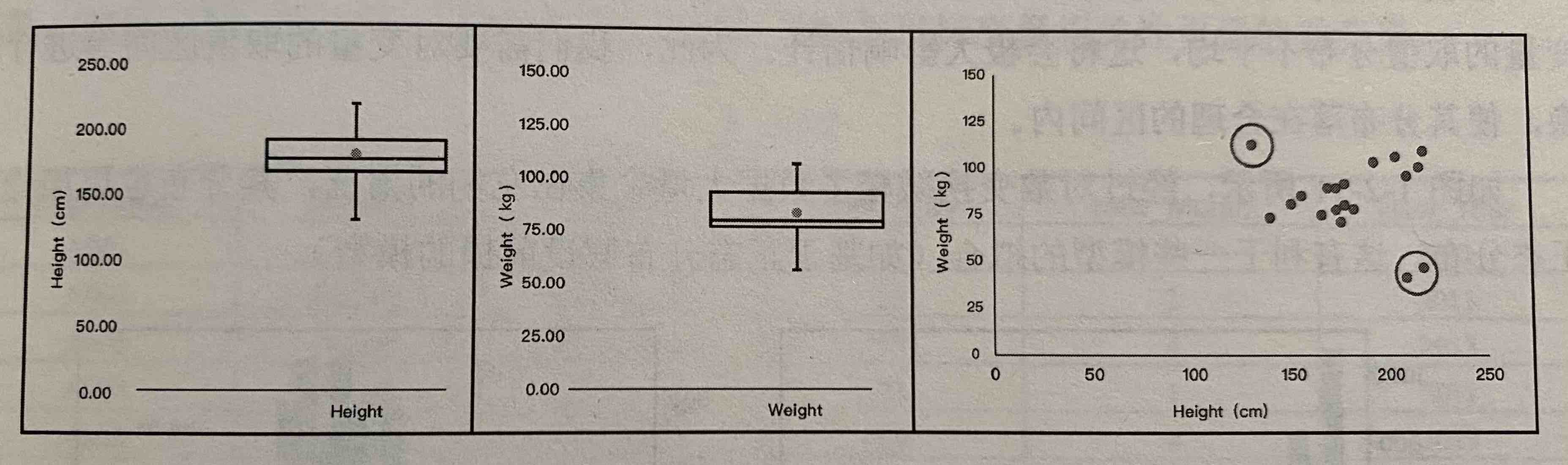
也可以使用散点图配合箱线图来判断,这里对于单变量height和weight都没有找到异常值,但是使用散点图看双变量分布,就可以看出来有两组样本是异常值。
异常值的处理方法
异常值的处理和缺失数据类似, 主要使用删除, 填充和区别对待的方法:
1.如果是由输入误差, 数据处理而产生的异常值, 或者异常值很小就可以直接删除
2. 如果是由自然产生的, 就可以像缺失数据一样, 使用均值, 中值进行填充,或者使用Capping的方法,比如大于95百分位的值都等于95百分位的值. 如果是人为产生的, 则可以使用预测模型进行填充.
3. 如果存在大量异常值, 就可以采用区别对待的方法, 将数据分为异常值和非异常值两组, 对两组分别进行建模, 最后将预测结果合并.